Synchronization Patterns in Transient Spiral Wave Dynamics
An important approach for analyzing spatially extended systems is “network analysis” (also called graphical methods) where time series are observed (or measured) at different spatial locations and then investigated with respect to potential interrelations between different parts or regions of the system. If strong relations are found this is often interpreted as being the result of structural inhomogeneities, hidden connections or other causalities. In view of applications to experimental heart data we have applied this approach to spatiotemporal dynamics of a homogeneous excitable medium exhibiting periodic dynamics in terms of (multiple) spiral waves (Fig. 1A; [1]). Time series were sampled on a (fine) grid of measurement points and mutually (cross) predicted using a nearest neighbor approach. Since the system is homogeneous with (global) periodic dynamics one would expect that all pairwise predictions provide similar errors. However, this is not the case. Instead we found regions of low mutual prediction errors separated by borders across which relatively high prediction errors are obtained (Fig. 1B). The origin of these patterns is a transient process during which regions of the excitable medium adjust their dynamics by fine-tuning their oscillation periods. Once this synchronization transient is over all patterns disappear and the network time series analysis provides the expected result (homogeneous cross prediction errors). However, convergence to this asymptotic state is very slow. Therefore, in particular in experiments, it is very likely that measurements are taken during the transient and may lead to wrong interpretations, for example concerning “inhomogeneity” of the underlying system or concerning additional connections between remote regions.
Figure 1
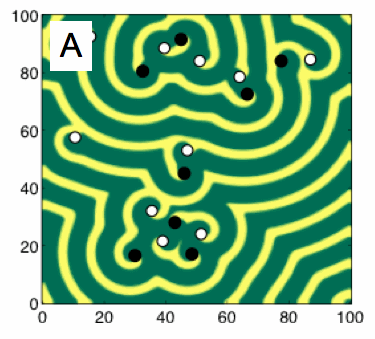
(A) Snapshot of the periodic spatiotemporal dynamics generated by the Barkley model. The black and white circles indicate phase singularities with clockwise and counter-clockwise rotation, respectively.
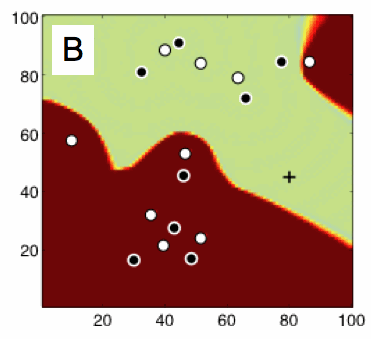
(B) Predictability chart of the Barkley model showing (color coded) averaged prediction errors at different spatial locations when using forecasts based on a time series from a given site indicated by +. Bright and dark colors correspond to low errors (<0.002) and high (>0.0024) prediction errors, respectively (from [1]).
References
- U. Parlitz, A. Schlemmer and S. Luther, Phys. Rev. E 83, 057201 (2011).